Press enter or click to view image in full size

Matrix Splines in Maya

Cole O'Brien

Follow

13 min read

·

Dec 20, 2020

56

1

With the release of Maya 2020, Autodesk included some new features enabling an improved matrix-based rigging workflow. Like many others this got me very excited about the future of rigging, as rigs entirely built with matrix connections would now be possible. However while solutions for constraints and IK solvers have been around for sometime, I had yet to see anyone attempt to replace Maya’s spline nodes.

Splines or NURBS are an essential tool for rigging spines, stretchy limbs or clothing. But when rigging with matrices they can be a bit awkward to work with. They require creating and storing dedicated DAG nodes somewhere in your scene, and they’re designed to work with vectors rather than matrices.

For past year I’ve experimented with building splines entirely with matrix connections. And over time the results have become more and more production viable. In this article I offer this matrix-friendly alternative that only uses vanilla Maya nodes. Even if this solution isn’t for you I hope this experiment can at least help demystify the math behind splines.

Overview

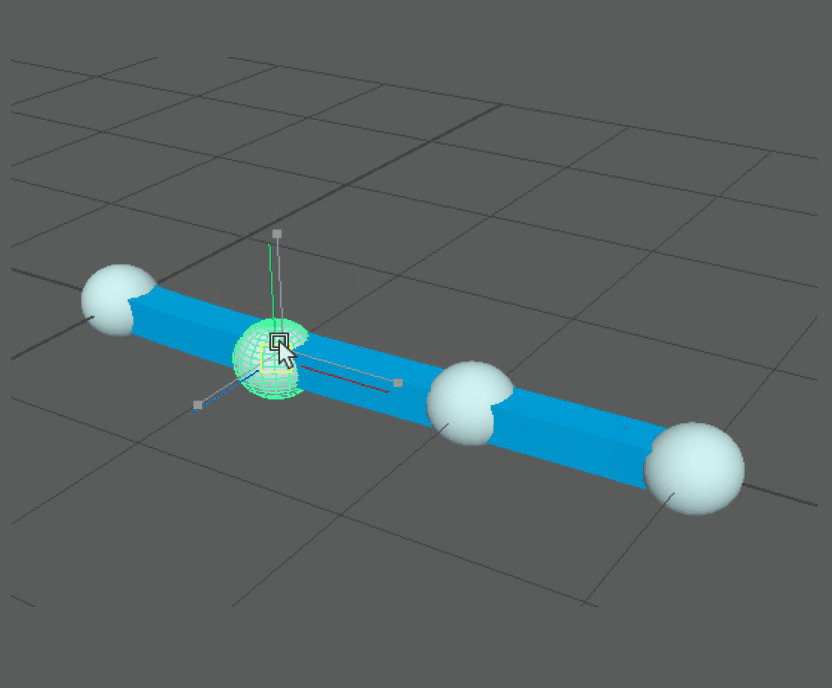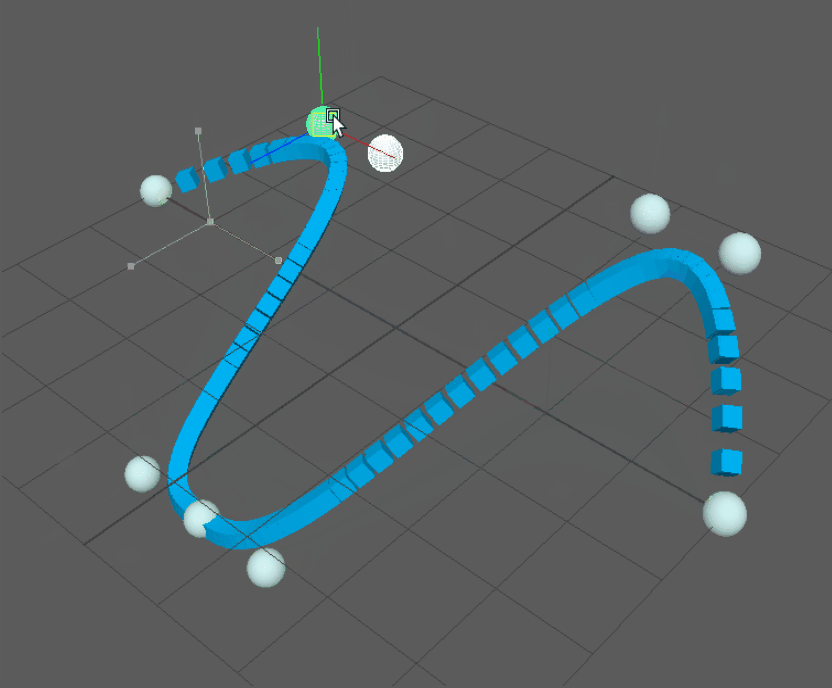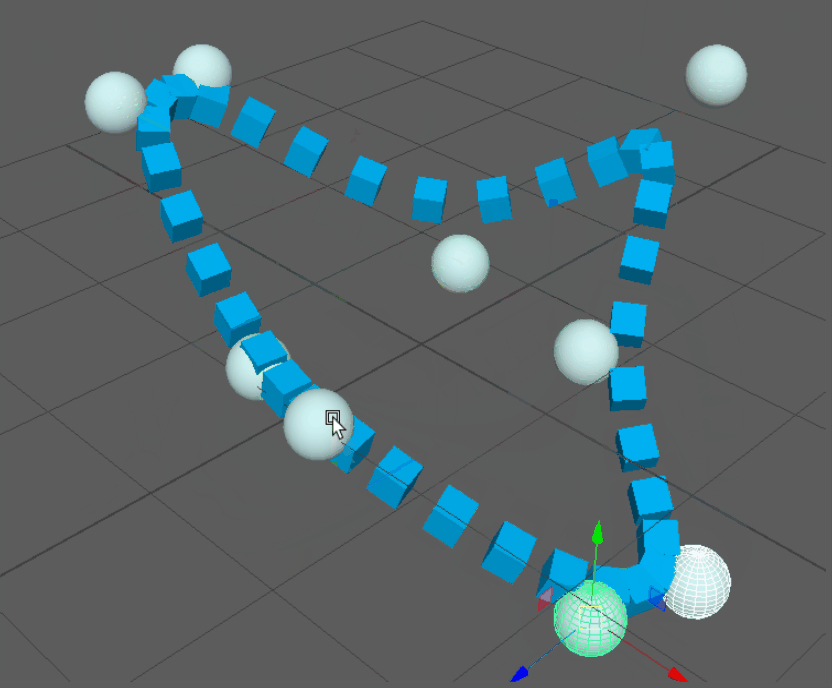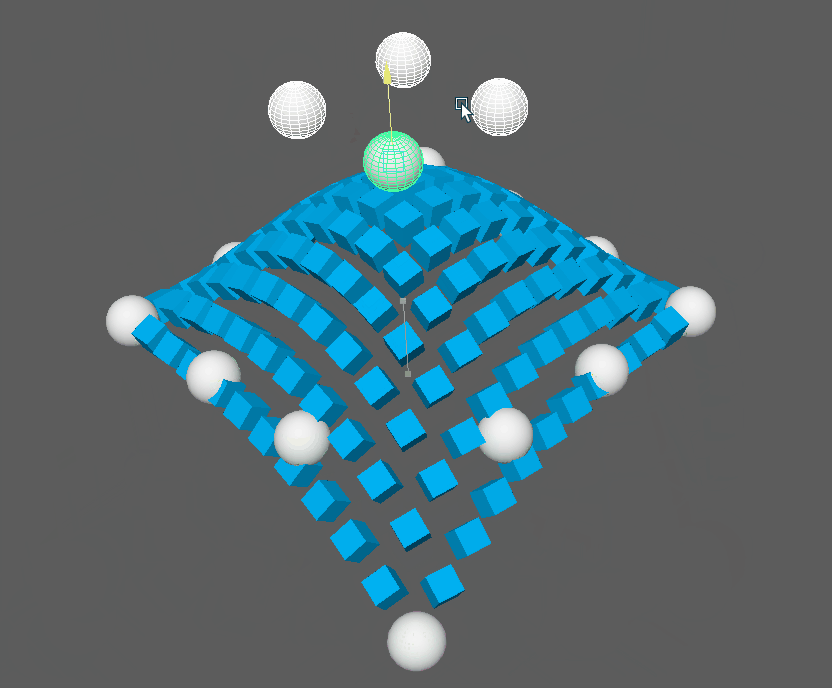
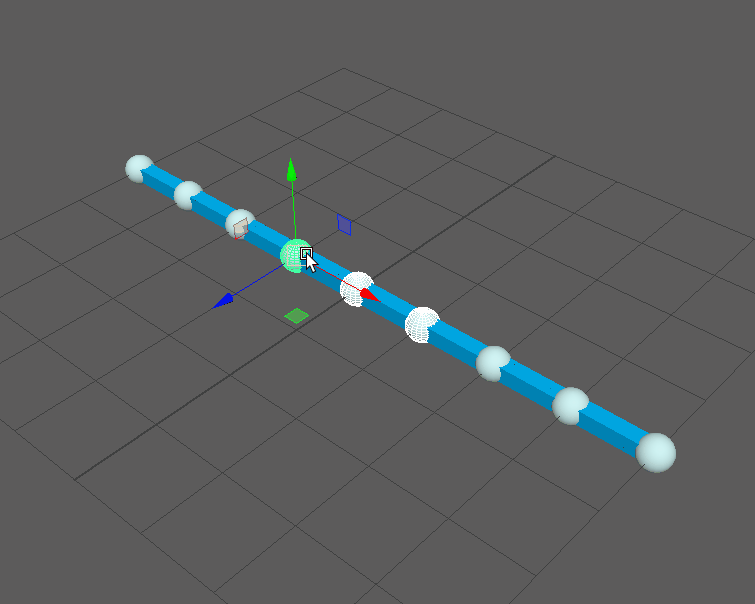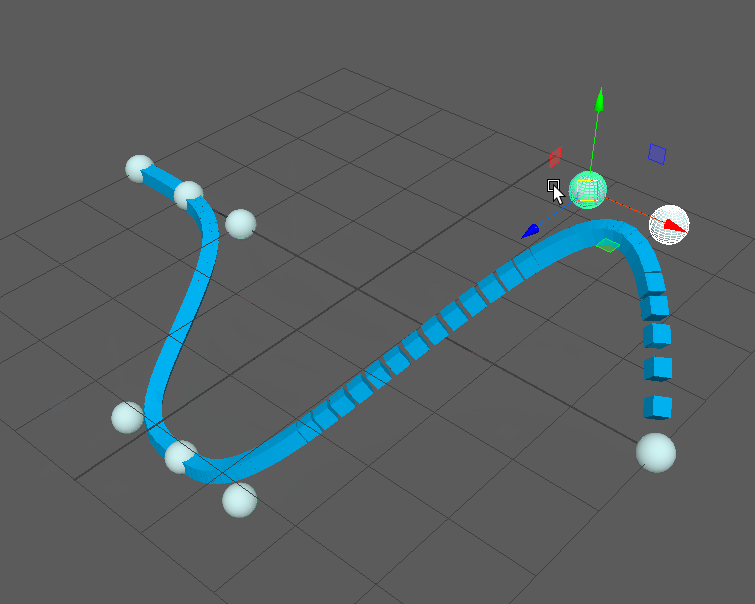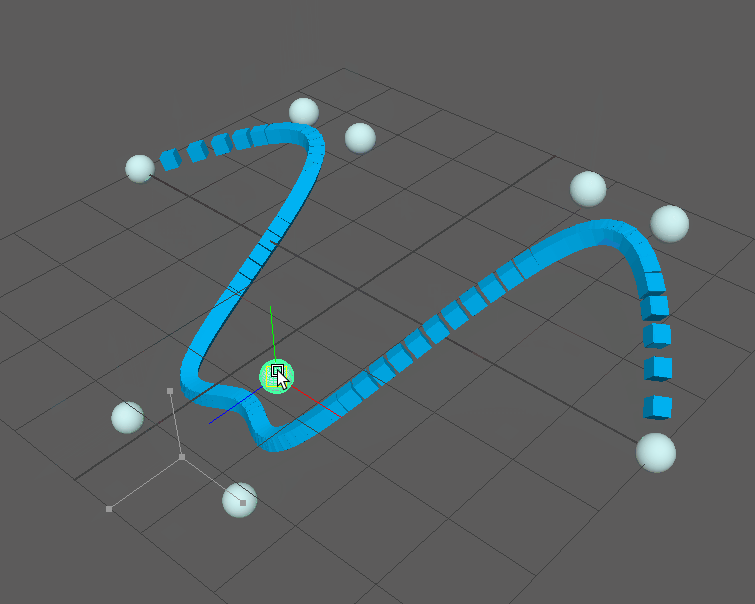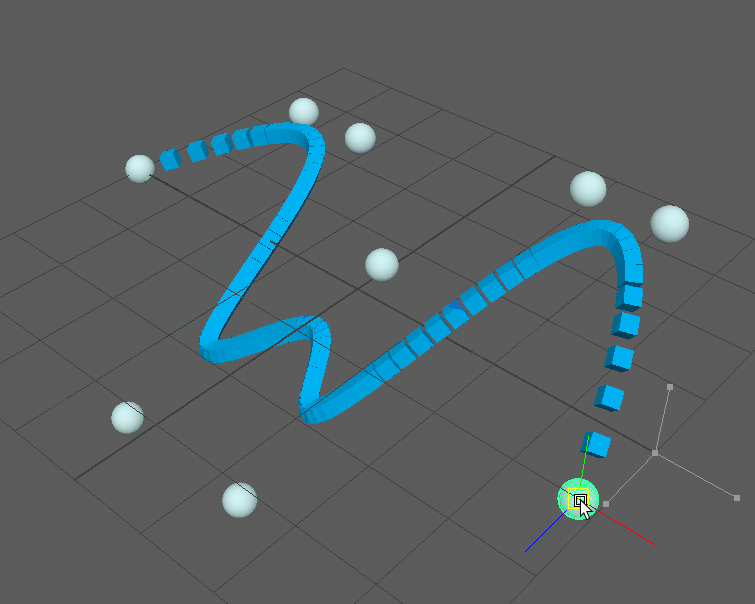
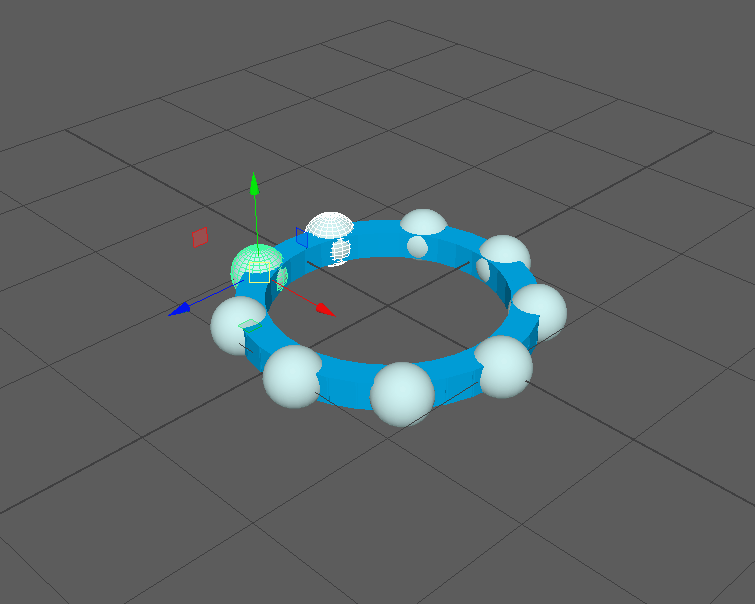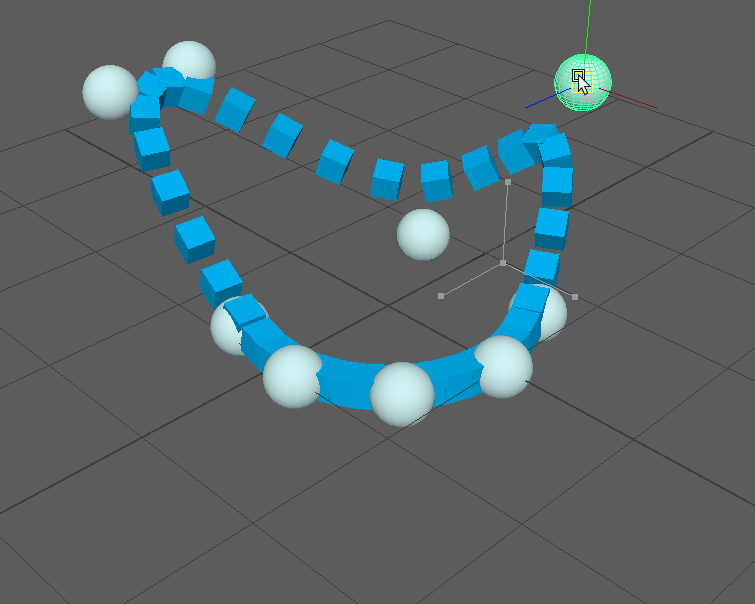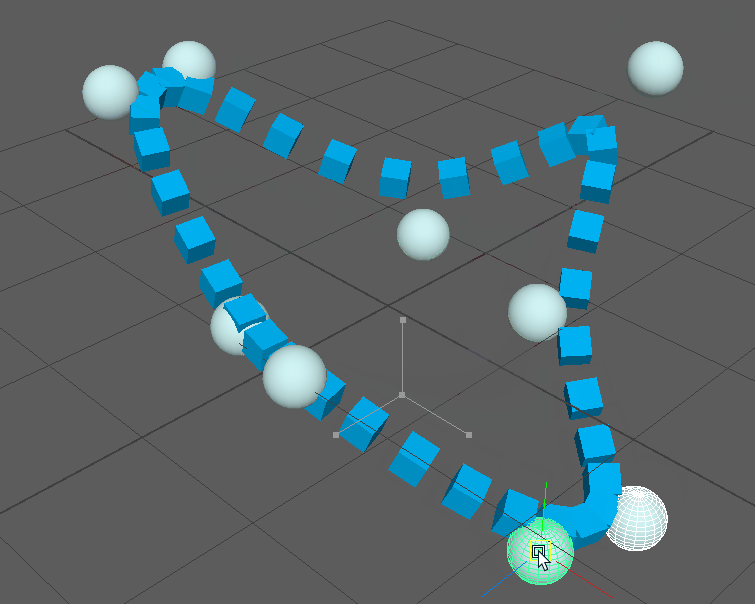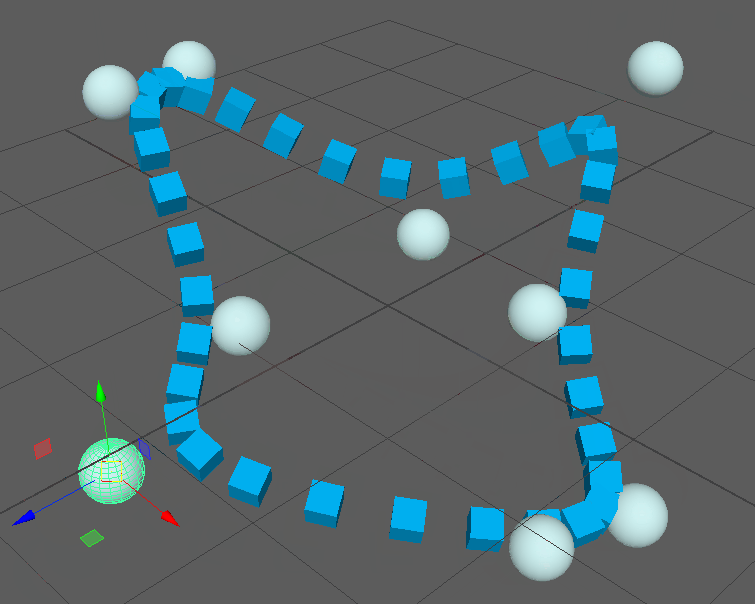
Before getting into the details of the setup, here’s a demo of the results in Maya. Note the absence of any nurbsCurve nodes in the outliner: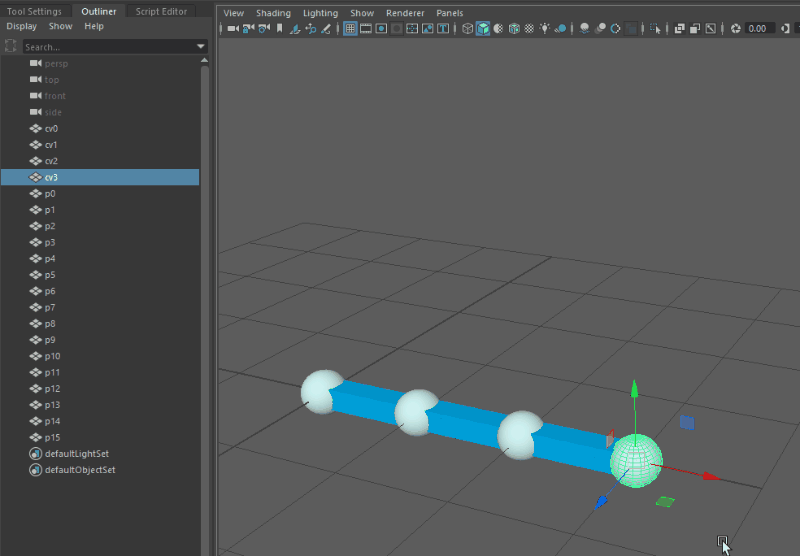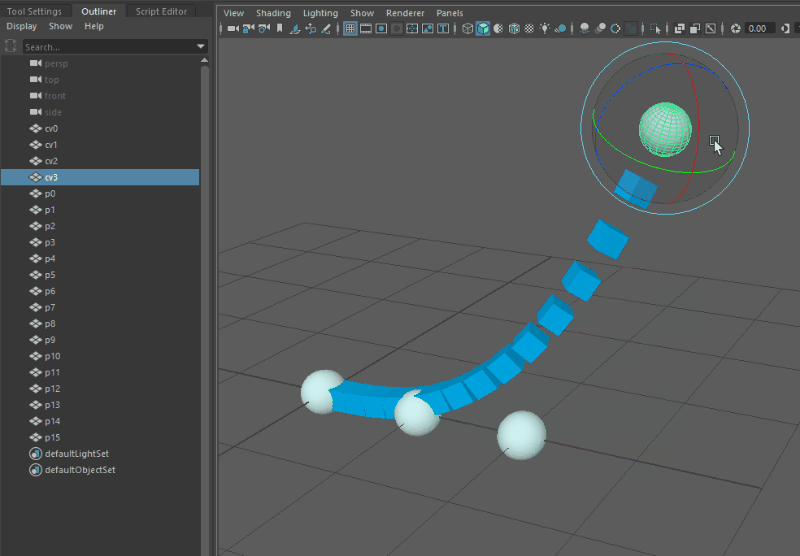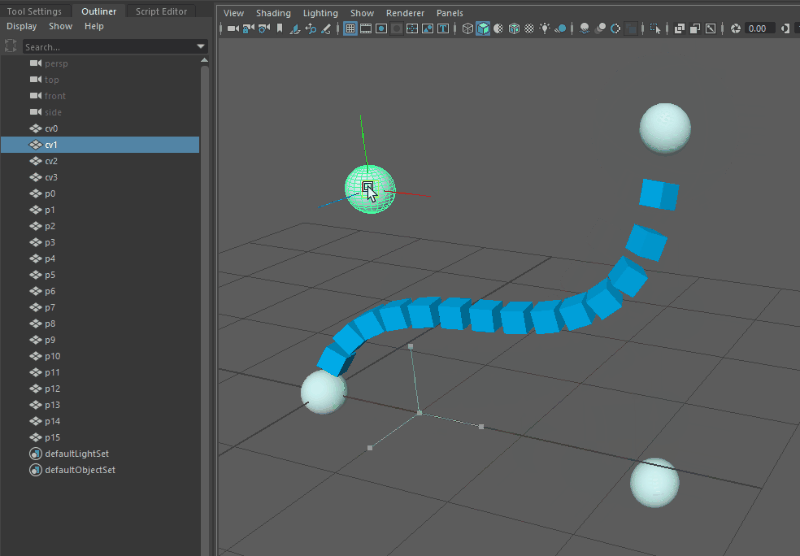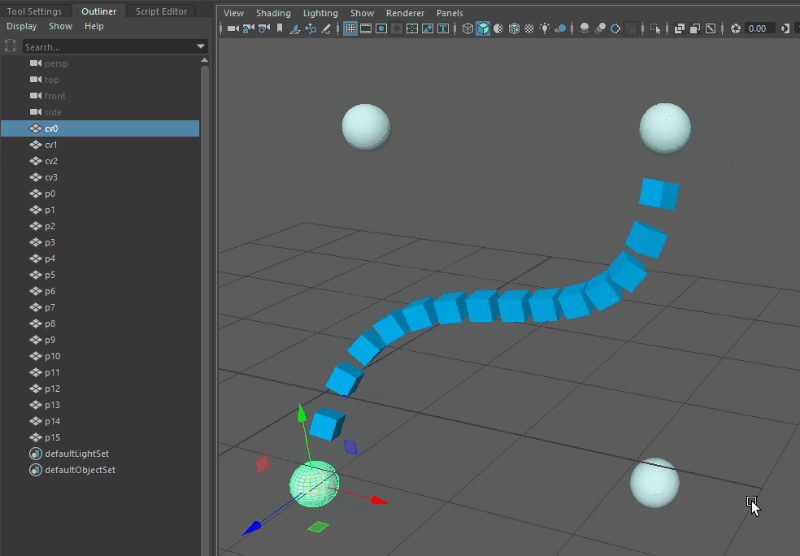

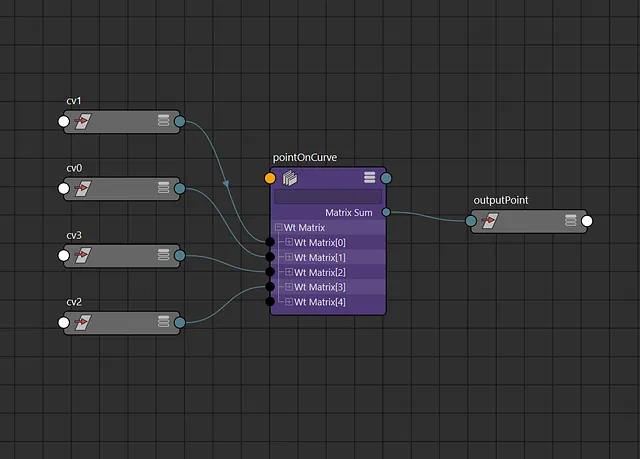
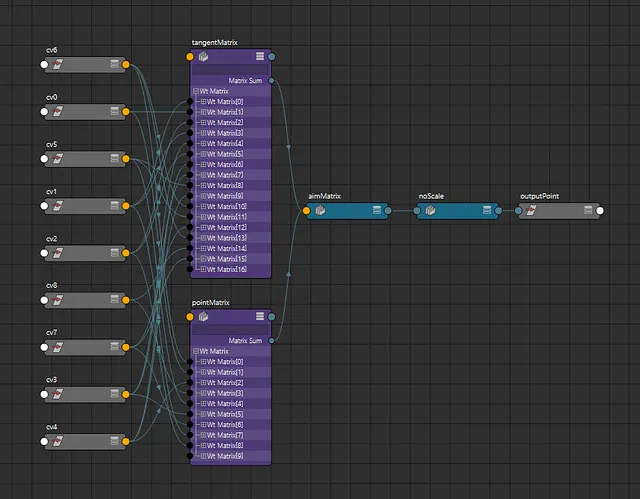
Press enter or click to view image in full size

But how does this implementation look in the node editor? Surprising the solution is fairly node-light and comparable to curveInfo node workflows. This is especially the case in Maya 2020 where we can take advantage of Maya’s new aimMatrix node. Here are the input connections for a single point on the curve: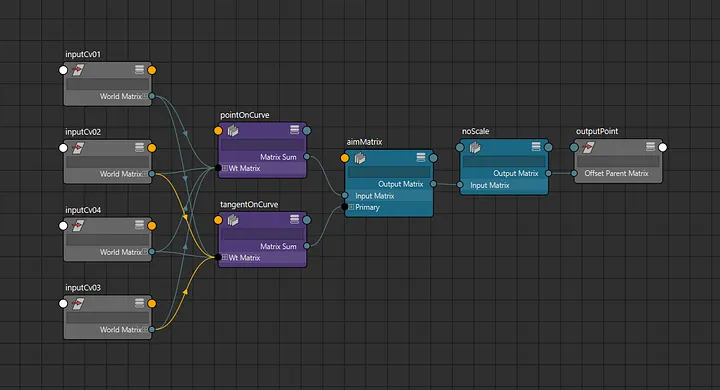

Press enter or click to view image in full size

Keep in mind that this is a complete NURBS implementation, so any amount of control points is supported as well as custom knot vectors for looping curves:

And this method doesn’t just work for curves, it supports surfaces as well:

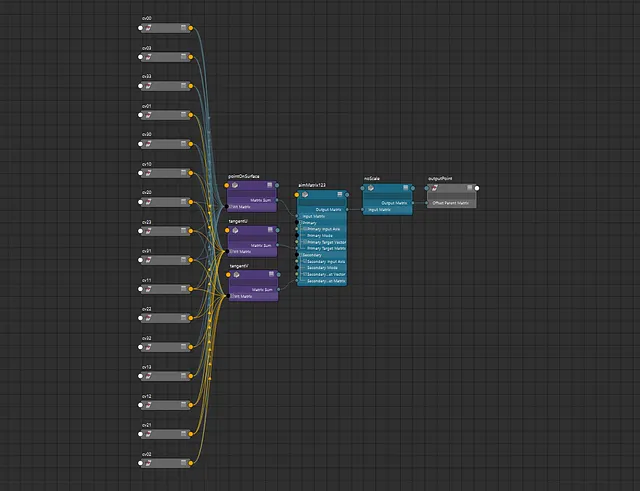
The secret ingredient here is Maya’s wtAddMatrix nodes. We use these nodes to obtain position and tangents on a curve in matrix form. However neither of these images are showing the entire picture. These nodes use specific weights generated from static parameter, degree and knot values.

I won’t get into the math just yet, but essentially by baking these parameters into weight values we can reduce the required operations down to weighted sums. While this simplifies our networks, it does unfortunately mean these values cannot be driven by attribute connections. Although it is possible for these operations to be replicated in node form, it would require far more connections and would hurt performance significantly.

Usage

While the actual node network setup is fairly simple, the matrix weights themselves are best generated through code. Fortunately I’ve wrapped all the math in as a python module.

This module contains several functions designed to generate control point or tangent weights for either spline curves or surfaces. Given a list of control points they will each return a mapping of control points to weight values. These functions are all written entirely in vanilla python as well, so they’re theoretically useable outside of a Maya context.

This output weight mapping can then be used to create a weighted sum. In Maya you essentially have two options for this. For matrices you’re limited to the previously mentioned wtAddMatrix node, but they theoretically could also work with the blendWeighted node for single dimensional values.

Keep in mind when using matrices the entire matrix will be blended. This can be handy using blended rotation for up vectors, but often scale will need to be picked out. Also the tangent matrices store the tangent value in the matrix translation rather than rotation. So in order to access this vector directly you will need to use a decomposeMatrix node.

The provided module also contains three functions for generating the example setups used for this article. Each function should work in both Maya 2020 and pre-2020. These example functions are intended for testing purposes or to serve as a starting point for use elsewhere. They are not designed to be fully functional auto-riggers though.

Advantages and Limitations

This method has a lot of advantages but its not the solution for every problem. While I’ve tested a similar method in production for the past year, I think its important to consider the pros and cons before implementing it.

Advantages

• Node Simplicity. There are many alternative methods to attach transforms to curves, but they often involve awkward conversions to and from NURBS nodes. All the heavy lifting here is done with a couple matrix nodes.
• Matrix Friendly. This method includes matrix inputs and outputs rather than vectors so its is perfect for use with the new matrix nodes in Maya 2020.
• No DAG Nodes. While hiding DAG nodes from your animators isn’t a huge problem, eliminating them certainly reduces outliner clutter and avoids infamous DO_NOT_TOUCH groups. This is also helpful when building rigs through code as there are no residual DAG nodes to worry about.
• Performance. I’m not an expert on testing performance but in my simple tests using dgtimer this setup performs almost 40x faster than using curveInfo nodes. Optimization wasn’t the goal of this workflow, but it is a nice perk!

Limitations

• Static parameter and knots. This is probably the biggest deal-breaker for anyone looking to implement this method. This means you cannot create rigs that slide along splines, or splines with locked lengths.
• Built-in Tool Support. Maya’s spline nodes include a lot of built-in utilities and tools that are incompatible with this workflow. This means we cannot drive curves with deformers or simulations, or use Maya’s API for querying curve data.
• Python Setup. While the provided module should be trivial to copy and paste where needed, if you’re used to rigging by hand this can be a bit of a burden.

Also I should also mention, a node plugin would probably be a lot more performant and create even simpler node networks. However if there’s one thing I’ve learned from working professionally is to avoid external dependencies. Creating rigs with plugins makes them harder to share and locks them to versions of Maya. For some pipelines plugins will be the solution but personally I always prefer a vanilla option.

Math Time

So far I’ve focused primarily on the practical applications of this method. But in the process of figuring this all out I’ve learned a lot about the math behind splines. While there are some great resources available online(this primer in particular was a huge help), they are often generalized or require extensive prior knowledge. So while I’m no expert, I feel like I should at least do my best to explain the math from a Maya rigging perspective.

Bezier Curves

Before I discuss splines, I should first go over Bezier curves. While these aren’t the same, understanding curves is fundamental to understanding splines.

One way to interpret a Bezier curve is as a weighted sum of control points. The amount of control points determines the curves order. In Maya though we often describe curves by their degree instead, which is one less than the order. So a curve with a degree of three will have four control points.

A position on a curve is described by a parameter or time(t) value. This single value often ranges from 0–1, starting at the first control point and terminating at the last. Bezier functions are essentially interpolation functions. In fact a degree two curve is essential a linear interpolation or a LERP function.

The equation itself for a Bezier curve is fairly simple. The formula on wikipedia for a degree 3 curve looks like this: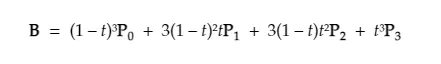

Where t is the parameter value, P are the input control points and B is the output Bezier point.

There’s really nothing too crazy about this formula, and should be pretty simple to convert into python code. Unfortunately, this format isn’t the most convenient to represent as a node network in Maya. Getting a single point will require around a dozen nodes just to add and multiply everything. Instead if we use a static time value we can simplify the equation into a weighted sum like this: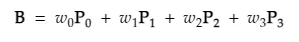

This is a lot better! And most importantly if we compose the points into matrices we can condense this equation into our single wtAddMatrix node. If we were to implement this function as is we’d get a network that looks like this:

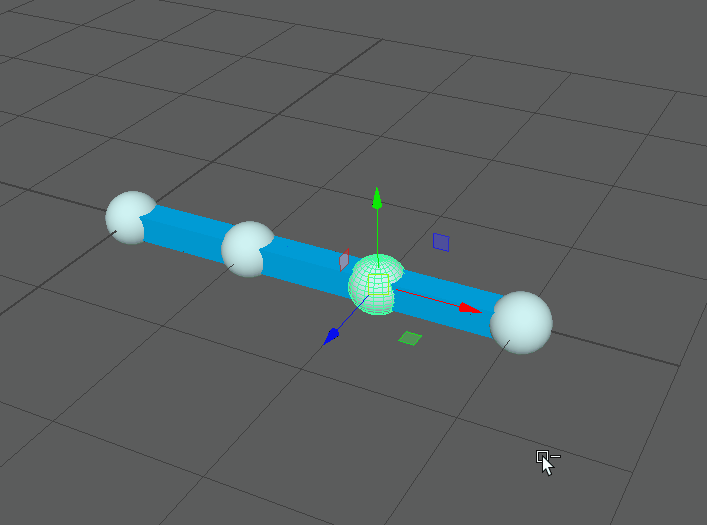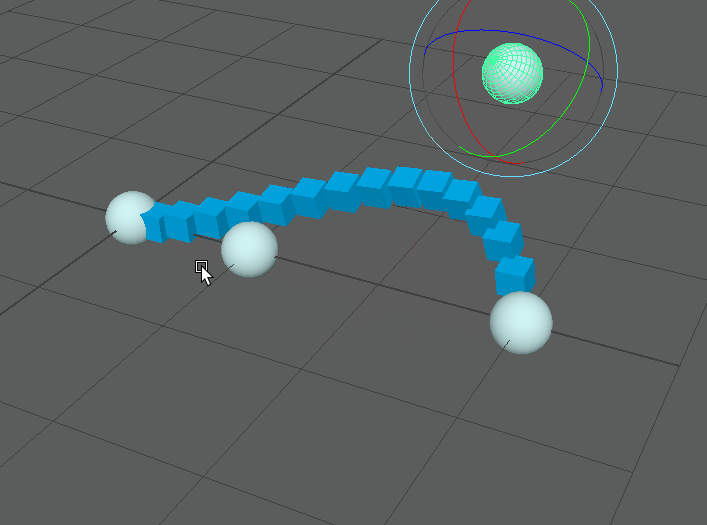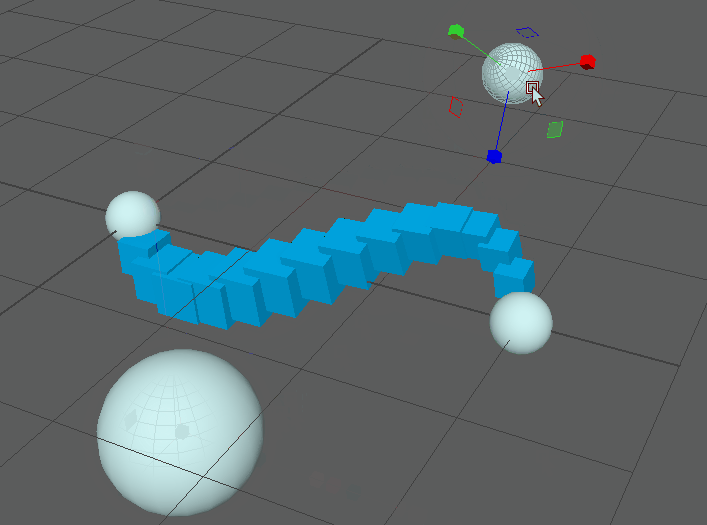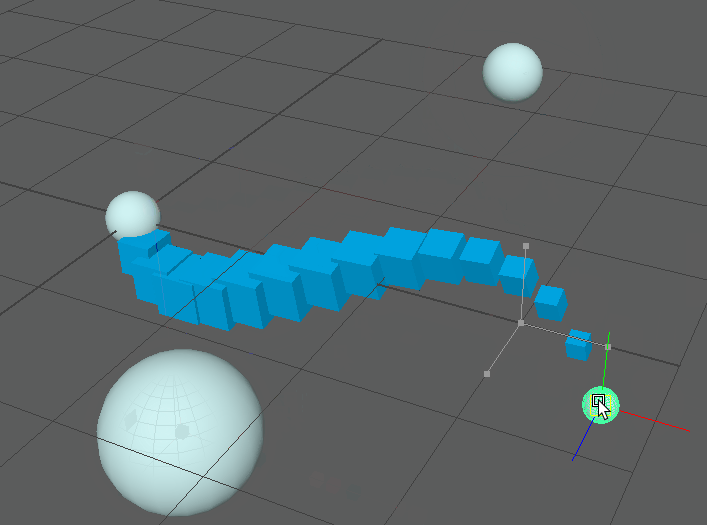
However we’re still missing a crucial element for spline rigs. Currently the attached points do not align with the curvature as we would expect. As mentioned earlier this process usually involves obtaining a tangent on the curve. This tangent vector and a well chosen up vector can be used to create a rotation matrix. This is covered in detail elsewhere, so instead I’ll focus on how we actually generate this tangent vector.

So what is a tangent exactly? Essentially this vector describes the rate of change at a point. In Calculus this is often referred to as the derivative of a function. Fortunately wikipedia also includes an equation for the Bezier derivative: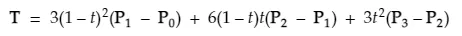

This may look like it’d be more complicated than the position equation, but it can actually be simplified down to a weighted sum of points as well: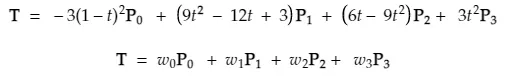

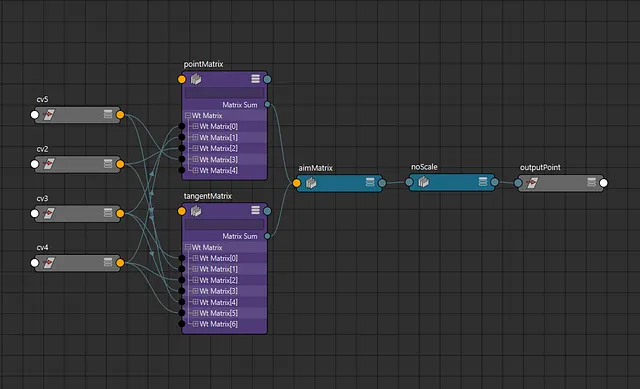
This means we can use the same control points with different weights to create a second matrix node for the tangent. Here’s what the results look like in Maya now:

At this point we could stop here as the results seem identical to the first example I showed, but we’re operating under a pretty strict limitation, the amount of control points is limited by the degree. So a degree three curve can only have four control points.

One solution to this problem could be to just use curves of increasing degree. This would allow us to add more control points, but the results are not ideal:

Besides impacting rig performance, the big problem for animation is that every control point affects every position on the curve. This is pretty wasteful and can can be un-intuitive to animate.

Another potential solution is we could add more Bezier curves, attaching them end to end. This could be preferable for some setups, but I find this adds too many control points and increases the complexity quite a bit. I would also prefer to avoid differentiating between which control points correspond to which curve.

I only mention this problem because its likely part of the reason Maya does not implement Bezier curves like this. Instead Autodesk uses a higher form of curve known as NURBS or splines!

Spline Curves

While Bezier curves can be interpreted as a method of interpolating points, NURBS can be considered a method of interpolating Bezier curves. NURBS stands for Non-Uniform Rational B-Splines, which is a lengthy way of saying it’s a type of spline. Splines solve our control point problem by using several curves blended together. So we can still have a degree three curve with more than four control points.

Here’s an example of a spline with the same control point count as before but with a degree of three. Note that each cube is now only affected by four control points:

So while splines seem more complicated, in practice they’re actual a lot lighter than Bezier curves! And since they’re still made from Bezier curves, any valid Bezier curve can be built as a spline. Maya’s version of “Bezier curves” are likely implemented as splines under the hood.

However in order to implement splines we need an updated formula that includes an additional parameter.

Knots

If you’ve ever written a curve serialization tool in Maya, you probably have worked with knots. Knots essentially describe the amount of influence each control point has on each part of a curve. They also allow us to modify our curves shape by adding corners or form loops. A basic knot vector might look something like this: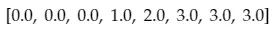

The length of this vector is determined by the curves degree and the number of control points like so: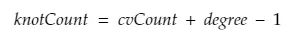

Press enter or click to view image in full size

This means the previous knot vector might describe a degree 3 curve with six control points. This spline would then contain three interpolated Bezier curves.

There seems to be a bit of an art to generating these vectors and I’m no expert, so I won’t go too in-depth. Still it can be helpful to know that repeated values will create corners or end points on your curve. The knot vector above has three repeated values at either end so that the curve terminates at the first and last control points. However a knot vector for a looping curve would not, and could look something like this: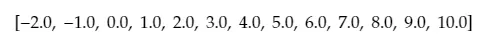

That said for most situations I use a script to auto generate my knots. I included the defaultKnots() function in the code provided that will handle knot generation. All the included functions will also generate default knots if none are provide. I still think it’s important to understand the value of a custom knot vector, as they can be pretty powerful for creating more complex curves.

Evaluating Splines

With an explanation of the knots out of the way, we can actually get into calculating a point on a spline. This is where things get a bit more complicated, and unlike Bezier curves I don’t think it’s very helpful to show the formula. Unlike Bezier curves we often use an algorithm to generate points on spline curves. Personally I used de Boor’s algorithm as the wikipedia page actually provided simple python code to implement it.

Similar to the Bezier formula, finding a tangent also consists of taking the derivative. While not as straight forward as with curves, I found a pretty helpful implementation on stack overflow.

This is also where it get a little more complicated in a Maya context. De Boors algorithm is recursive and finds a point over many iterations. This process is optimized for finding a point in code, but doesn’t lend itself to creating node networks in Maya. Fortunately I created a modified version that will generate weights for each control point instead. This can be found in the pointOnCurveWeights() and tangentOnCurveWeights() functions in the provided code.

This is also why limiting our curves to static knots and parameters is especially important for splines. The amount of operations can be extensive and would likely impact performance. Each point on a spline would also require connections from every control point, defeating a bit of the purpose.

Spline Surfaces

With the bulk of the math explanation over with, I’d like to conclude with a quick explanation of surfaces as well. While they might seem to be more complicated than spline curves, they’re actually quite similar and only require one additional matrix node.

Essentially a spline surface is made of rows and columns of control points. These points are shared to create overlapping splines.

To find a position on a surface we’ll need two parameters instead of one. Maya calls these the u and v parameters and that’s what I used in the provided code. We’ll also need two sets of knot vectors as well, one for the rows and another for the columns. Keep in mind at least with my implementation, all rows must have the same length as well as the columns.

Using these two parameters we can find the control point weights for the row and column splines separately. Then we just multiply them together to get the final weight. While most of the heavy lifting is done in the curve functions, I included dedicated surface weight function sin the provided code.

For surfaces we also end up with two tangents instead of one. This actually can simplify our node networks a little as we no longer need an up vector. These can be plugged in as primary and secondary matrices in Maya’s aimMatrix node or decomposed to be assembled manually.

Conclusion

Before this experiment I expected splines to much more complex than they actually are. After investigating it turns out they can be distilled into simple weighted sums. And once I realized this, I started to notice this pattern everywhere in rigging. Dot products, matrix multiplication, RBF solvers, and skin weights are all just forms of weighted sums!

However I’ll save those topics for a future article. I’m sure after I publish this I’ll stumble upon another method that’s better in every way. Nevertheless I hope this explanation helps more tech animators understand the math behind their rigs. Rigging in Maya is filled with abstracted math and I strongly feel the closer we get to understanding the fundamental principles the better!